
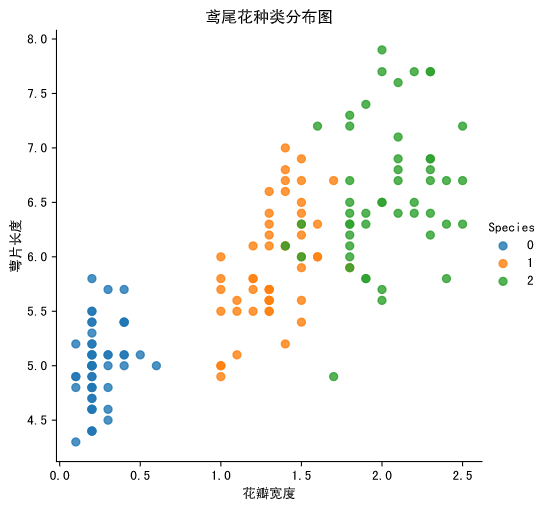
算法原理
一句话概括:相似的事物彼此接近。
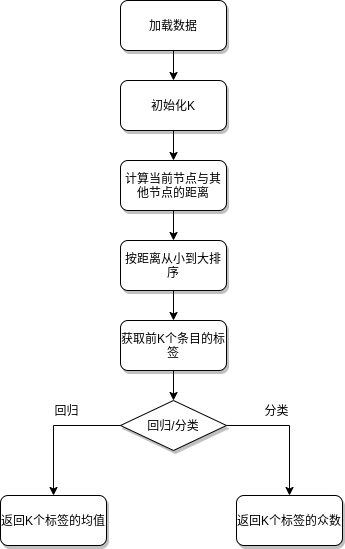
距离度量
欧式距离
欧氏距离是最容易直观理解的距离度量方法,两个点在空间中的距离一般都是指欧氏距离。
曼哈顿距离(Manhattan Distance)
在曼哈顿街区要从一个十字路口开车到另一个十字路口,驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是“曼哈顿距离”。曼哈顿距离也称为“城市街区距离”(City Block distance)。

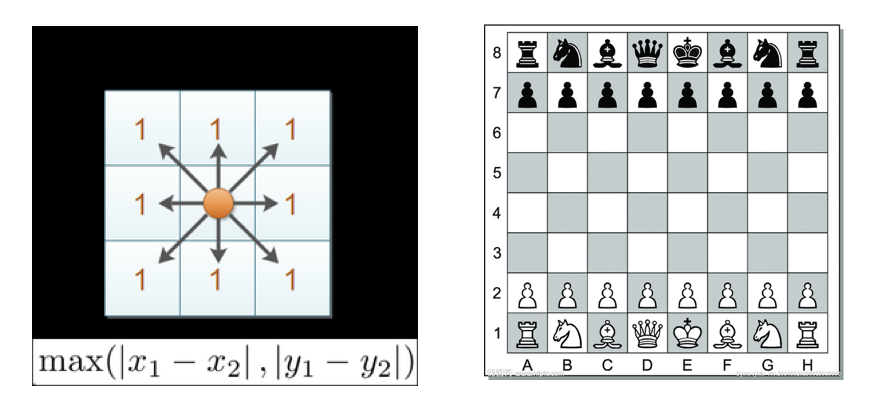
切比雪夫距离 (Chebyshev Distance):
国际象棋中,国王可以直行、横行、斜行,所以国王走一步可以移动到相邻8个方格中的任意一个。国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步?这个距离就叫切比雪夫距离。
余弦距离(Cosine Distance)
几何中,夹角余弦可用来衡量两个向量方向的差异;机器学习中,借用这一概念来衡量样本向量之间的差异。
- 二维空间中向量A(x1,y1)与向量B(x2,y2)的夹角余弦公式:
- 两个n维样本点a(x11,x12,…,x1n)和b(x21,x22,…,x2n)的夹角余弦为:
夹角余弦取值范围为[-1,1]。余弦越大表示两个向量的夹角越小,余弦越小表示两向量的夹角越大。当两个向量的方向重合时余弦取最大值1,当两个向量的方向完全相反余弦取最小值-1。
代码实现
手动实现
from collections import Counter
import math
def knn(data, query, k, distance_fn, choice_fn):
neighbor_distances_and_indices = []
# 3. 对于数据中的每个例子
for index, example in enumerate(data):
# 3.1 计算查询示例与当前的距离
# 来自数据的示例。
distance = distance_fn(example[:-1], query)
# 3.2 将示例的距离和索引添加到有序集合中
neighbor_distances_and_indices.append((distance, index))
# 4. 对有序的距离和索引集合进行排序
# 按距离最小到最大(按升序)
sorted_neighbor_distances_and_indices = sorted(neighbor_distances_and_indices)
# 5. 从排序集合中挑选前 K 个条目
k_nearest_distances_and_indices = sorted_neighbor_distances_and_indices[:k]
# 6. 获取选中的 K 个条目的标签
k_nearest_labels = [data[i][-1] for distance, i in k_nearest_distances_and_indices]
# 7.如果回归(choice_fn = mean),返回K个标签的平均值
# 8.如果分类(choice_fn = mode),返回K个标签的模式
return k_nearest_distances_and_indices , choice_fn(k_nearest_labels)
def mean(labels):
return sum(labels) / len(labels)
def mode(labels):
return Counter(labels).most_common(1)[0][0]
def euclidean_distance(point1, point2):
sum_squared_distance = 0
for i in range(len(point1)):
sum_squared_distance += math.pow(point1[i] - point2[i], 2)
return math.sqrt(sum_squared_distance)
def main():
'''
# 回归数据
#
# 第 0 列:高度(英寸)
# 第 1 列:重量(磅)
'''
reg_data = [
[65.75, 112.99],
[71.52, 136.49],
[69.40, 153.03],
[68.22, 142.34],
[67.79, 144.30],
[68.70, 123.30],
[69.80, 141.49],
[70.01, 136.46],
[67.90, 112.37],
[66.49, 127.45]
]
# 问题:
# 根据我们拥有的数据,如果某人身高 60 英寸,那么对他们的体重的最佳猜测是什么?
reg_query = [60]
reg_k_nearest_neighbors, reg_prediction = knn(
reg_data, reg_query, k=3, distance_fn=euclidean_distance, choice_fn=mean
)
'''
# 分类数据
#
# 第 0 列:年龄
# 第 1 列:喜欢菠萝
'''
clf_data = [
[22, 1],
[23, 1],
[21, 1],
[18, 1],
[19, 1],
[25, 0],
[27, 0],
[29, 0],
[31, 0],
[45, 0],
]
# 问题:
# 根据我们掌握的数据,33 岁的人喜欢披萨上的菠萝吗?
clf_query = [13]
clf_k_nearest_neighbors, clf_prediction = knn(
clf_data, clf_query, k=3, distance_fn=euclidean_distance, choice_fn=mode
)
if __name__ == '__main__':
main()
sklearn实现
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV
# 1、获取数据集
iris = load_iris()
# 2、数据基本处理 -- 划分数据集
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)
# 3、特征工程:标准化
# 实例化一个转换器类
transfer = StandardScaler()
# 调用fit_transform
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 4、KNN预估器流程
# 4.1 实例化预估器类
estimator = KNeighborsClassifier()
# 4.2 模型选择与调优——网格搜索和交叉验证
# 准备要调的超参数
param_dict = {"n_neighbors": [1, 3, 5]}
estimator = GridSearchCV(estimator, param_grid=param_dict, cv=3)
# 4.3 fit数据进行训练
estimator.fit(x_train, y_train)
# 5、评估模型效果
# 方法a:比对预测结果和真实值
y_predict = estimator.predict(x_test)
print("比对预测结果和真实值:\n", y_predict == y_test)
# 方法b:直接计算准确率
score = estimator.score(x_test, y_test)
print("直接计算准确率:\n", score)
特征缩放
特征的单位或者大小相差较大,或者某特征的方差相比其他的特征要大出几个数量级,容易影响(支配)目标结果,使得一些算法无法学习到其它的特征
特征预处理API
sklearn.preprocessing
sklearn.preprocessing 模块包括缩放、居中、归一化、二值化方法。
归一化
对数值类型的特征做归一化可以将所有的特征都统一到一个大致相同的数值
区间内。最常用的方法主要有以下两种。
线性函数归一化(Min-Max Scaling)。它对原始数据进行线性变换,使结果映射到[0, 1]的范围,实现对原始数据的等比缩放。归一化公式如下
$$
X_{'} = \frac{X-X_}{X_-X_} \
X{''} = X^{'}*(X_-X_)+X_
$$
其中X为原始数据,、分别为数据最大值和最小值,为最终结果
API
sklearn.preprocessing.MinMaxScaler(feature_range=0, 1, *, copy=True, clip=False)fit_transform(X, y=None, **fit_params)
注意最大值最小值是变化的,另外,最大值与最小值非常容易受异常点影响,所以这种方法鲁棒性较差,只适合传统精确小数据场景。
标准化
零均值归一化(Z-Score Normalization)。它会将原始数据映射到均值为0、标准差为1的分布上。具体来说,假设原始特征的均值为μ、标准差为σ,那么归一化公式定义为
-
对于归一化来说:如果出现异常点,影响了最大值和最小值,那么结果显然会发生改变
-
对于标准化来说:如果出现异常点,由于具有一定数据量,少量的异常点对于平均值的影响并不大,从而方差改变较小。
-
sklearn.preprocessing.StandardScaler(*, copy=True, with_mean=True, with_std=True)fit_transform(X, y=None, **fit_params)
示例代码
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import StandardScaler
def minmax_demo():
"""
归一化演示
:return: None
"""
data = pd.read_csv("../data/dating.txt")
print(data)
# 1、实例化一个转换器类
transfer = MinMaxScaler(feature_range=(2, 3))
# 2、调用fit_transform
data = transfer.fit_transform(data[['milage','Liters','Consumtime']])
print("最小值最大值归一化处理的结果:\n", data)
return None
def stand_demo():
"""
标准化演示
:return: None
"""
data = pd.read_csv("../data/dating.txt")
print(data)
# 1、实例化一个转换器类
transfer = StandardScaler()
# 2、调用fit_transform
data = transfer.fit_transform(data[['milage','Liters','Consumtime']])
print("标准化的结果:\n", data)
print("每一列特征的平均值:\n", transfer.mean_)
print("每一列特征的方差:\n", transfer.var_)
return None
minmax_demo()
print('\n==================================================\n')
stand_demo()
示例数据
milage,Liters,Consumtime,target
40920,8.326976,0.953952,3
14488,7.153469,1.673904,2
26052,1.441871,0.805124,1
75136,13.147394,0.428964,1
38344,1.669788,0.134296,1
72993,10.141740,1.032955,1
35948,6.830792,1.213192,3
42666,13.276369,0.543880,3
67497,8.631577,0.749278,1
35483,12.273169,1.508053,3
50242,3.723498,0.831917,1
63275,8.385879,1.669485,1
5569,4.875435,0.728658,2
51052,4.680098,0.625224,1
77372,15.299570,0.331351,1
43673,1.889461,0.191283,1
61364,7.516754,1.269164,1
69673,14.239195,0.261333,1
15669,0.000000,1.250185,2
28488,10.528555,1.304844,3
6487,3.540265,0.822483,2
......
交叉验证
交叉验证:将拿到的训练数据,分为训练和验证集。以下图为例:将数据分成4份,其中一份作为验证集。然后经过4次(组)的测试,每次都更换不同的验证集。即得到4组模型的结果,取平均值作为最终结果。又称4折交叉验证。

网格搜索(Grid Search)
通常情况下,有很多参数是需要手动指定的(如k-近邻算法中的K值),这种叫超参数。但是手动过程繁杂,所以需要对模型预设几种超参数组合。每组超参数都采用交叉验证来进行评估。最后选出最优参数组合建立模型。

示例代码
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV
# 1、获取数据集
iris = load_iris()
# 2、数据基本处理 -- 划分数据集
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)
# 3、特征工程:标准化
# 实例化一个转换器类
transfer = StandardScaler()
# 调用fit_transform
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 4、KNN预估器流程
# 4.1 实例化预估器类
estimator = KNeighborsClassifier()
# 4.2 模型选择与调优——网格搜索和交叉验证
# 准备要调的超参数
param_dict = {"n_neighbors": [1, 3, 5]}
estimator = GridSearchCV(estimator, param_grid=param_dict, cv=3)
# 4.3 fit数据进行训练
estimator.fit(x_train, y_train)
# 5、评估模型效果
# 方法a:比对预测结果和真实值
y_predict = estimator.predict(x_test)
print("比对预测结果和真实值:\n", y_predict == y_test)
# 方法b:直接计算准确率
score = estimator.score(x_test, y_test)
print("直接计算准确率:\n", score)
参考资料
- https://towardsdatascience.com/machine-learning-basics-with-the-k-nearest-neighbors-algorithm-6a6e71d01761
- https://zhuanlan.zhihu.com/p/23191325
- https://scikit-learn.org/stable/modules/neighbors.html
- https://dl.acm.org/doi/10.1145/361002.361007
- http://stanford.edu/class/archive/cs/cs106l/cs106l.1162/handouts/assignment-3-kdtree.pdf
