
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
当我们需要设计一个线性函数()去拟合一些呈线性关系的数据点时,我们如何评价我们设计的拟合函数的拟合效果呢?换言之,我们如何评价我们设计的拟合函数与实际值的差距、损失?
一个直接的思路是计算所有实际点到拟合函数的距离的和:
显然,这种计算方式有除法,开根号,开方,非常的复杂,耗时,不可取。
损失计算函数应当尽量简单且能直观反映损失。
通常使用如下函数来评价损失
$y_i$是实际值,$f(x_i)$是拟合函数预测值。通过计算两者的差值的平方(取绝对值会更复杂)来评判单个点的拟合损失,对所有结果求和来评判整体的拟合效果
$L(a, b)$是一个二元函数,我们的目标就是求$L(a, b)$的最小值,即$\min L(a, b)$时$a,b$的取值,这时也是拟合效果最好的。
要求$L$的最小值,问题就转化为求$L$的偏导数(神经网络中称为梯度)
$$
\left{ \begin
\frac{\partial L}{\partial b} = 0
\end\frac{\partial L}{\partial a} = 0 \ \right.
$$
用数学语言表示直线:参数化 $y = ax+b$ 
指定标准:建立评价函数 $L(a, b)$
已知数据点(0, 1), (1, 2), (2, 4),求线性函数$f(x)=ax+b$
Step1: 构造评价函数
$$
L(a, b) = \sum_N (y_i - f(x_i))2 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ L(a, b) = (1-b)2+(2-(a+b))2+(4-(2a+b))^2
$$
Step2: 分别对于a和b合并同类项,整理成二次函数形式
$$
g_1(a) = (1-b)2 + (2-(a+b))2 + (4 - (2a+b))2 \
g_2(b) = 3b2 + (6a-14)b + (5a^2 -20a + 21)
$$
Step3: 求二次方法构造二元一次方程组求出a、b
$$
\left{ \begin
b = -\frac{6a-14}{6}
\enda = -\frac{6b-20}{10} \ \right.
\implies
\left{ \begin
b = \frac{5}{6} \enda = \frac{3}{2} \ \right.
$$
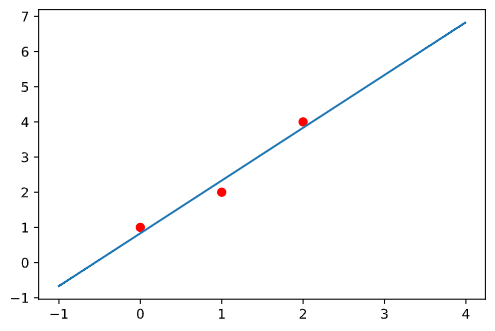
最小二乘法的几何意义
是n维欧式空间的点集,$\vec a$处$x$的观测值,$\vec b$是对应的拟合值
$$
S= {P_i(x_i, y_i)} \
\vec a = (y_1, y_2, y_3, ..., y_n) \in \mathbb
\vec b = (f(x_i), f(x_2), f(x_3), ..., f(x_n)) \in \mathbb \
\
拟合\Leftrightarrow | \vec a - \vec b |2 = (y_1-f(x_1))2 + (y_2-f(x_2))2 + (y_3-f(x_3))2 + ... + (y_n-f(x_n))^2 = L
$$
最小二乘法的几何意义就是去寻找n维空间上点的最小距离,让这两个点的距离尽可能的小。距离越小,拟合的效果就越好。
最小二乘法的非线性拟合
最小二乘法的一个本质难点就是函数型的选取。对于非线性函数, 我们可以将它划分成非常小的一段,这一段可以用线性函数来拟合。这种思想在定积分中也有应用。

在神经网络中通常使用激活函数来引入非线性因素用以拟合各种曲线。
常用的激活函数有: $sigmoid, tanh, RELU, LeakReLu, SoftMax$等等
$$
sigmoid: \ \ \ \ f(x) = \frac{1}{1+e^{-x}}
$$
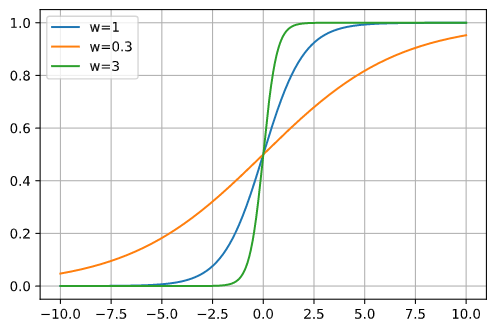

如下图所示:
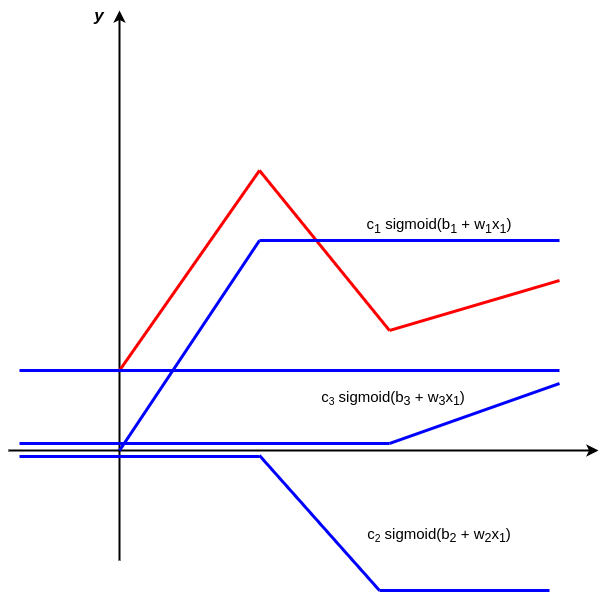
图中红色曲线可以通过其他三条蓝色曲线“组合”而成。
总结
| 优点 | 缺点 | 适用性 |
|---|---|---|
| 1. 反映综合趋势 | ||
| 2. 具有强几何意义 | ||
| 3. 具有强统计意义 | 1. 难以选取函数型 | |
| 2. 对于含有指数和对数型的拟合函数难以计算参数 | 1. 适用于预测 | |
| 2. 某些情况下也可以做插值 |
