
之前的分类模型写完后同学问我有没有回归的模型评价方法,现在,它来了 
刚开始,我直接搜索回归模型的评价方法有哪些,但是突然想起来之前学习线性回归模型的时候有用到均方误差计算损失,于是猜想sklearn中十有八九有提供相应的损失评价方法,于是
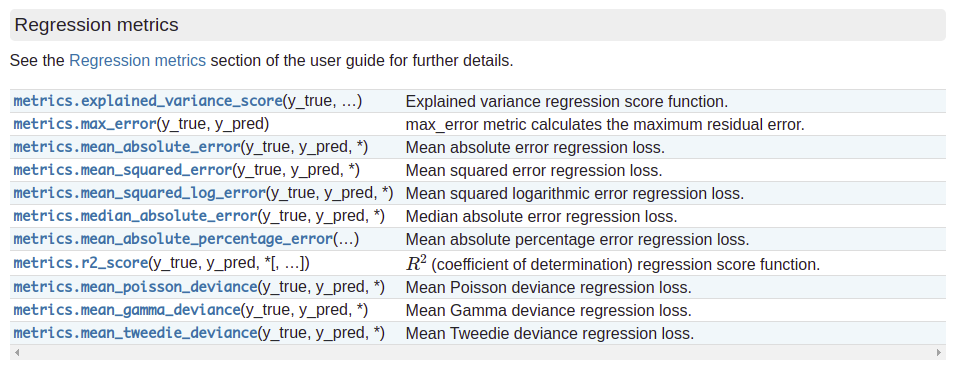
一共提供有11种方法

接下来对每个方法简单介绍,最后给出相关示例代码。
之前介绍的最小二乘法用来计算拟合误差是一个理论上的方法,在实际情况中有很大的局限性:
$$
\sum_m (y_{(i)} - \hat y_{(i)})2
$$
值的大小和样本数量 m 有密切关系,这样的结果是无法衡量模型好坏的。
举个例子,假设建立了两个模型,一个模型使用了 10 个样本,计算出的上式值是 100;另一个模型使用了 50 个样本,计算出的值是 200,很难判断两个模型哪个更好。
下面的几种方法其实都是建立在最小二乘法的基础上,不断改进的。
MSE(均方误差)
$MSE (Mean Squared Error)$ 的原理就是将上式除以m以消除样本数量的影响
$$
MSE = \frac{1} \sum_m (y_{(i)} - \hat y_{(i)})2
$$
RMSE
$MSE$ 公式有一个问题是会改变量纲。因为公式平方了,比如说 y 值的单位是万元,$MSE$ 计算出来的是万元的平方,对于这个值难以解释它的含义。所以为了消除量纲的影响,我们可以对这个$MSE$ 开方,得到的结果就第二个评价指标:均方根误差 $RMSE(Root Mean Squared Error)$
$$
\sqrt{\frac{1}\sum_\left(y_{\text }{(i)}-\hat{\text }{(i)}\right){2}}=\sqrt{M S E{\text }}= RM S E_{\text }
$$
可以看到 $MSE$ 和 $RMSE$ 二者是呈正相关的,$MSE$ 值大,$RMSE$ 值也大,所以在评价线性回归模型效果的时候,使用 RMSE 就可以了。
MAE
上面公式为了避免误差出现正负抵消的情况,采用计算差值的平方。还有一种公式也可以起到同样效果,就是计算差值的绝对值:
$$
\sum_^ |y_i - \hat y_i |
$$
因此,将上式也除以样本数 m 得到的结果就是第三个评价指标:平均绝对误差 MAE(Mean Absolute Error):
$$
\frac{1} \sum_^ |y_i - \hat y_i | = MAE
$$
上面三个模型解决了样本数量 m 和 量纲的影响。但是它们都存在一个相同的问题:当量纲不同时,难以衡量模型效果好坏。
R2_score
它的含义就是,既然不同数据集的量纲不同,很难通过上面的三种方式去比较,那么不妨找一个第三者作为参照,根据参照计算 R方值,就可以比较模型的好坏了。
这个参照是什么呢,就是均值模型。我们知道一份数据集是有均值的,房价数据集有房价均值,学生成绩有成绩均值。现在我们把这个均值当成一个基准参照模型,也叫 baseline model。这个均值模型对任何数据的预测值都是一样的,可以想象该模型效果自然很差。基于此我们才会想从数据集中寻找规律,建立更好的模型。
$$
R2 = 1 - \frac{\sum_i (\hat y{(i)} - y{(i)})2}{\sum_i (\overline y - y{(i)})2}
$$
**R2_score = 1,达到最大值。**即分子为 0 ,意味着样本中预测值和真实值完全相等,没有任何误差。也就是说我们建立的模型完美拟合了所有真实数据,是效果最好的模型,R2_score 值也达到了最大。但通常模型不会这么完美,总会有误差存在,当误差很小的时候,分子小于分母,模型会趋近 1,仍然是好的模型,随着误差越来越大,R2_score 也会离最大值 1 越来越远,直到出现第 2 中情况。
R2_score = 0**。此时分子等于分母,样本的每项预测值都等于均值。也就是说我们辛苦训练出来的模型和前面说的均值模型完全一样,还不如不训练,直接让模型的预测值全去均值。当误差越来越大的时候就出现了第三种情况。
R2_score < 0 :分子大于分母,训练模型产生的误差比使用均值产生的还要大,也就是训练模型反而不如直接去均值效果好。出现这种情况,通常是模型本身不是线性关系的,而我们误使用了线性模型,导致误差很大。
理解了 R2_score 后,我们可以对它的计算公式作进一步改进,以便后面编程实现。将分子和分母同除以一个 m,就能得到下式:
$$
R2 = 1 - \frac{\frac {\sum_i (\hat y{(i)} - y{(i)})2}}{\frac {\sum_i (\overline y - y{(i)})2}} = 1- \frac{MSE(\hat y, y)}{Var(y)}
$$
分子是均方误差,分母是方差,都能直接计算得到,从而能快速计算出 R2 值。
Explained variance score(解释方差得分)
可解释变异(英语:explained variation)在统计学中是指给定数据中的变异能被数学模型所解释的部分。通常会用方差来量化变异,故又称为可解释方差(explained variance)。
除可解释变异外,总变异的剩余部分被称为未解释变异(unexplained variation)或残差(residual)。
线性回归中的决定系数即为可解释变异占总变异的比率。
$$
explained_{}variance(y, \hat) = 1 - \frac{Var{ y - \hat}}{Var{y}}
$$
$\hat y$是预测值,$y$是真实目标值,$Var$是方差
最好的分数是 1.0,值越低表示模型性能越差。
手动实现
import pandas as pd
y_true = pd.Series([3, -0.5, 2, 7])
y_pred = pd.Series([2.5, 0.0, 2, 8])
explained_variance_score = 1 - (y_true - y_pred).var()/y_true.var()
print(explained_variance_score)
# 0.9571734475374732
Max error(最大误差)
这是一个衡量预测值和真实值之间最坏情况误差的指标。在完美拟合的单输出回归模型中,训练集上的 max_error 将为 0,尽管这在现实世界中极不可能发生,但该指标显示了模型在拟合时的误差程度。
如果$\hat y_i$ 是第 i 个样本的预测值,并且$y_i$ 是对应的真值,那么最大误差定义为
$$
\text(y, \hat) = max(| y_i - \hat_i |)
$$
手动实现
import pandas as pd
y_true = pd.Series([3, 2, 7, 1])
y_pred = pd.Series([9, 2, 7, 1])
max_error = (y_true - y_pred).abs().max()
print(max_error)
# 6
Mean absolute error(平均绝对误差)
Mean absolute error,平均绝对误差,听名字就知道啥意思,不解释
$$
\text(y, \hat) = \frac{1}{n_{\text}} \sum_^{n_{\text}-1} \left| y_i - \hat_i \right|.
$$
手动实现
import pandas as pd
y_true = pd.Series([3, -0.5, 2, 7])
y_pred = pd.Series([2.5, 0.0, 2, 8])
mean_absolute_error = (y_true - y_pred).abs().mean()
print(mean_absolute_error)
# 0.5
Mean squared logarithmic error(均方对数误差)
$$
\text(y, \hat) = \frac{1}{n_\text} \sum_{n_\text - 1} (\ln (1 + y_i) - \ln (1 + \hat_i) )2.
$$
当目标呈指数增长时,最好使用该指标,例如人口数量、商品在几年内的平均销售额等。请注意,该指标对低估估计的惩罚大于高估估计。
手动实现
import pandas as pd
import numpy as np
y_true = pd.Series([3, 5, 2.5, 7])
y_pred = pd.Series([2.5, 5, 4, 8])
mean_squared_log_error = ((1 + y_true).apply(np.log) - (1 + y_pred).apply(np.log)).pow(2).mean()
print(mean_squared_log_error)
# 0.03973012298459379
Mean absolute percentage error(平均绝对百分比误差)
$$
\text(y, \hat) = \frac{1}{n_{\text}} \sum_^{n_{\text}-1} \frac{{}\left| y_i - \hat_i \right|}{max(\epsilon, \left| y_i \right|)}
$$
手动实现
import pandas as pd
import numpy as np
y_true = pd.Series([1, 10, 1e6])
y_pred = pd.Series([0.9, 15, 1.2e6])
epsilon = np.finfo(np.float64).eps
mean_absolute_percentage_error = (y_true - y_pred).abs().div(np.maximum(epsilon, y_true.abs())).mean()
print(mean_absolute_percentage_error)
# 0.26666666666666666
Median absolute error(中值绝对误差)
medium_absolute_error 特别有趣,因为它对异常值具有鲁棒性。损失是通过取目标和预测之间所有绝对差异的中位数来计算的。
$$
\text(y, \hat) = \text(\mid y_1 - \hat_1 \mid, \ldots, \mid y_n - \hat_n \mid).
$$
手动实现
import pandas as pd
import numpy as np
y_true = pd.Series([3, -0.5, 2, 7])
y_pred = pd.Series([2.5, 0.0, 2, 8])
median_absolute_error = (y_true - y_pred).abs().median()
print(median_absolute_error)
# 0.5
Mean Poisson, Gamma, and Tweedie deviances(平均泊松、伽玛和特威迪偏差)
mean_tweedie_deviance 函数使用幂参数 (p) 计算平均 Tweedie 偏差误差。这是一个引出回归目标的预测期望值的指标。
- 当 power=0 时,它相当于 mean_squared_error。
- 当 power=1 时,它相当于 mean_poisson_deviance。
- 当 power=2 时,它相当于 mean_gamma_deviance。
$$
\begin\text(y, \hat) = \frac{1}{n_\text}
\sum_{n_\text - 1}
\begin
(y_i-\hat_i)2, & \text
2(y_i \log(y/\hatp=0\text{ (Normal)}\_i) + \hat_i - y_i), & \text
2(\log(\hat \ p=1\text{ (Poisson)}\_i/y_i) + y_i/\hat_i - 1), & \text \ p=2\text{ (Gamma)}\
2\left(\frac{\max(y_i,0){2-p}}{(1-p)(2-p)}-
\frac{y,\hat{1-p}_i}{1-p}+\frac{\hat^{2-p}_i}{2-p}\right),
& \text
\end\end
$$
Tweedie 偏差是 2 次幂的齐次函数。因此,power=2 的 Gamma 分布意味着同时缩放 y_true 和 y_pred 对偏差没有影响。对于 Poisson 分布 power=1,偏差线性缩放,对于正态分布(power=0),二次缩放。通常,功率越高,真实目标和预测目标之间的极端偏差的权重就越小。
上面这段话翻译自官网,意思就是当p=0时,mean tweedie deviance等价于$MSE$;当p=1时等价于(mean_poisson_deviance)平均泊松偏差;当p=2时,等价于平均伽马偏差。前两个对真实值的绝对误差,相对误差都很敏感,而gamma deviance只对相对误差敏感
下面是官网给的一个例子用以说明在p不同时mean_tweedie_deviance对误差的敏感度
p = 0
>>> from sklearn.metrics import mean_tweedie_deviance
>>> mean_tweedie_deviance([1.0], [1.5], power=0)
0.25
>>> mean_tweedie_deviance([100.], [150.], power=0)
2500.0
p = 1
>>> from sklearn.metrics import mean_tweedie_deviance
>>> mean_tweedie_deviance([1.0], [1.5], power=0)
0.25
>>> mean_tweedie_deviance([100.], [150.], power=0)
2500.0
p = 2
>>> mean_tweedie_deviance([1.0], [1.5], power=2)
0.14...
>>> mean_tweedie_deviance([100.], [150.], power=2)
0.14...
波士顿房价案例
下面以波士顿房价为例,使用线性回归模型分析,并使用以上损失评价方法进行检验
# 导入相关包
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import explained_variance_score, max_error, mean_absolute_error, mean_squared_error, mean_squared_log_error, median_absolute_error, mean_absolute_percentage_error, r2_score, mean_poisson_deviance, mean_gamma_deviance, mean_tweedie_deviance
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import SGDRegressor
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
boston_data = load_boston()
boston_data.keys()
# dict_keys(['data', 'target', 'feature_names', 'DESCR', 'filename'])
data = boston_data.data
target = boston_data.target
feature_names = boston_data.feature_names
# 拆分成训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(data, target, random_state=22)
# 特征工程-标准化
scaler = StandardScaler()
X_train = scaler.fit_transform(X=X_train)
X_test = scaler.fit_transform(X=X_test)
# 梯度下降回归模型
estimator = SGDRegressor(max_iter=1000,eta0=0.01)
# 训练
estimator.fit(X=X_train, y=y_train)
# 查看回归系数
estimator.coef_
# 获取预测值
y_predict = estimator.predict(X=X_test)
# 下面是损失计算方法
explained_variance_score(y_true=y_test, y_pred=y_predict) # 0.7605088603443888
max_error(y_true=y_test, y_pred=y_predict) # 17.245389826740357
mean_absolute_error(y_true=y_test, y_pred=y_predict) # 3.355693963657288
mean_squared_error(y_true=y_test, y_pred=y_predict) # 20.20727165845424
mean_squared_log_error(y_true=y_test, y_pred=y_predict) # 0.05325335547097157
median_absolute_error(y_true=y_test, y_pred=y_predict) # 2.7659956889047166
mean_absolute_percentage_error(y_true=y_test, y_pred=y_predict) # 0.17311944049045486
r2_score(y_true=y_test, y_pred=y_predict) # 0.7591300362244477
mean_poisson_deviance(y_true=y_test, y_pred=y_predict) # 0.964081584965728
mean_gamma_deviance(y_true=y_test, y_pred=y_predict) # 0.07827366055029722
mean_tweedie_deviance(y_true=y_test, y_pred=y_predict) # 20.20727165845424
搞完,歇会~~
