在模型评估过程中，分类问题、排序问题、回归问题往往需要使用不同的指标进行评估。在诸多的评估指标中，大部分指标只能片面地反映模型的一部分性能。如果不能合理地运用评估指标，不仅不能发现模型本身的问题，而且会得出错误的结论。

与线性回归问题不同，分类问题，或者说逻辑回归问题输出的是离散值，即判断某件事物属于哪个类别。事实上，逻辑回归模型输出的是一个概率值，通过将这个概率预测值与设定的分类阈值（threshold）进行比较，若大于阈值则分为正类，否则为反类。

评价指标

准确率（Accuracy），精确率（Precision），召回率（Recall），均方根误差 （Root Mean Square Error，RMSE）

准确率

$$
Accuracy = \frac{n_}{n_}

$$

其中$n_$为被正确分类的样本个数，$n_$为总样本的个数。

准确率是分类问题中最简单也是最直观的评价指标，但存在明显的缺陷。比如，当负样本占99%时，分类器把所有样本都预测为负样本也可以获得99%的准确 率。所以，当不同类别的样本比例非常不均衡时，占比大的类别往往成为影响准 确率的最主要因素。

精确率（Precision）

精确率也叫查准率，表示预测结果为正例样本中真实为正例的比例。

混淆矩阵（混淆矩阵也称误差矩阵，是表示精度评价的一种标准格式，用n行n列的矩阵形式来表示）

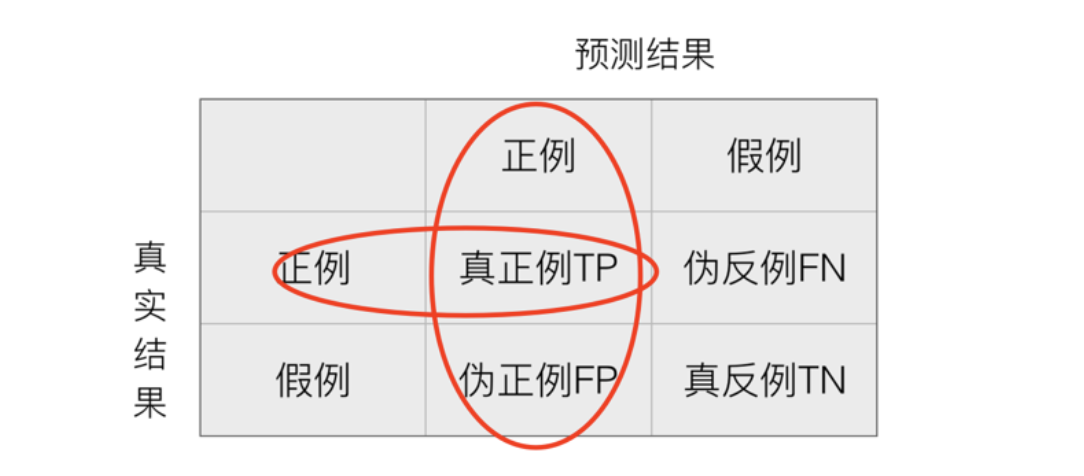
召回率(Recall)

召回率也叫查全率，表示真实为正例的样本中预测结果为正例的比例（查得全，对正样本的区分能力）

F1 score

F1 score是精确率和召回率的调和平均值

$$
\begin

&= \frac{2TP}{2TP + FN + FP}
\endF1 &= \frac{2*precision * recall}{precision + recall} \

$$

P-R曲线

P-R曲线的横轴是召回率，纵轴是精确率。对于一个排序模型来说，其P-R曲线上的一个点代表着，在某一阈值下，模型将大于该阈值的结果判定为正样本， 小于该阈值的结果判定为负样本，此时返回结果对应的召回率和精确率。整条P-R 曲线是通过将阈值从高到低移动而生成的。

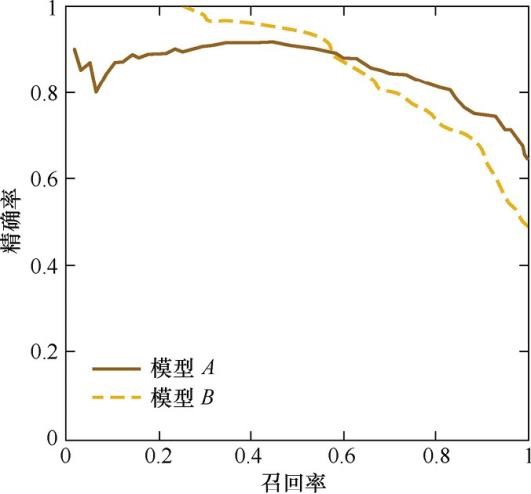
由图可见，当召回率接近于0时，模型A的精确率为0.9，模型B的精确率是1， 这说明模型B得分前几位的样本全部是真正的正样本，而模型A即使得分最高的几个样本也存在预测错误的情况。并且，随着召回率的增加，精确率整体呈下降趋 势。但是，当召回率为1时，模型A的精确率反而超过了模型B。这充分说明，只用某个点对应的精确率和召回率是不能全面地衡量模型的性能，只有通过P-R曲线的 整体表现，才能够对模型进行更为全面的评估。

RMSE

$$
RMSE = \sqrt{\sum_^n (y_i - \hat y_i)}

$$

其中，$y_i$是第i个样本点的真实值， 是第i个样本点的预测值，n是样本点的个数。

一般情况下，RMSE能够很好地反映回归模型预测值与真实值的偏离程度。但 在实际问题中，如果存在个别偏离程度非常大的离群点（Outlier）时，即使离群点数量非常少，也会让RMSE指标变得很差。

ROC曲线

ROC曲线是Receiver Operating Characteristic Curve的简称，中文名为“受试者工作特征曲线”。ROC曲线源于军事领域，而后在医学领域应用甚广，“受试者工作 特征曲线”这一名称也正是来自于医学领域。

ROC曲线的横坐标为假阳性率（False Positive Rate，FPR）；纵坐标为真阳性 率（True Positive Rate，TPR）。FPR和TPR的计算方法分别为

$$
\begin{align*}
FPR = \frac = \frac
TPR = \frac{TP + FN} \ = \frac{TN+FP}
\end{align*}

$$

上式中，P是真实的正样本的数量，N是真实的负样本的数量，TP是P个正样本中 被分类器预测为正样本的个数，FP是N个负样本中被分类器预测为正样本的个 数。

ROC曲线是通过不断移动分类器的“截断点”来生成曲线上的一组关 键点的，通过动态地调整截断点，从最高的得分开始（实际上是从正无穷开始，对应 着ROC曲线的零点），逐渐调整到最低得分，每一个截断点都会对应一个FPR和 TPR，在ROC图上绘制出每个截断点对应的位置，再连接所有点就得到最终的 ROC曲线。

AUC

AUC指的是ROC曲线下的面积大小，该值能够量化地反映基于 ROC曲线衡量出的模型性能。计算AUC值只需要沿着ROC横轴做积分就可以了。 由于ROC曲线一般都处于$y=x$这条直线的上方（如果不是的话，只要把模型预测的 概率反转成1−p就可以得到一个更好的分类器），所以AUC的取值一般在0.5～1之 间。AUC越大，说明分类器越可能把真正的正样本排在前面，分类性能越好。

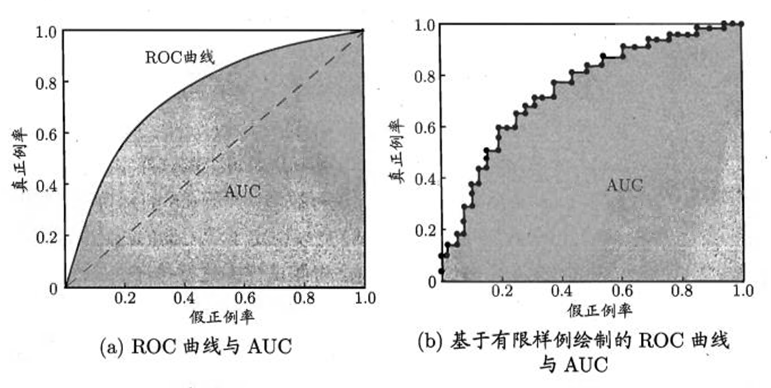
下面通过代码演示下各种曲线的绘制，以下代码参考了sklearn官方示例，对于各种指标sklearn中都有提供相关的可视化方法，直接调用就好。

  • 加载数据集
## Load Data and train model
# 对于本示例，我们从 OpenML <https://www.openml.org/d/1464> 加载输血服务中心数据集。这是一个二元分类问题，目标是个人是否献血。然后将数据拆分为训练数据集和测试数据集，并使用训练数据集拟合逻辑回归。

from sklearn.datasets import fetch_openml
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split

X, y = fetch_openml(data_id=1464, return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y)

clf = make_pipeline(StandardScaler(), LogisticRegression(random_state=0))
clf.fit(X_train, y_train)
  • 展示混淆矩阵
# 使用拟合模型，我们计算模型对测试数据集的预测。这些预测用于计算使用 :class:ConfusionMatrixDisplay 绘制的混淆矩阵
from sklearn.metrics import confusion_matrix
from sklearn.metrics import ConfusionMatrixDisplay

y_pred = clf.predict(X_test)
cm = confusion_matrix(y_test, y_pred)

cm_display = ConfusionMatrixDisplay(cm).plot()

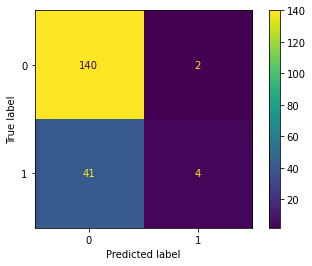
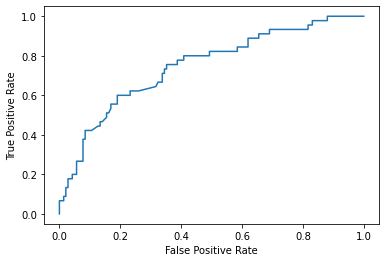
  • 绘制ROC曲线
# roc 曲线需要来自估计器的概率或非阈值决策值。由于逻辑回归提供了一个决策函数，我们将使用它来绘制 roc 曲线：
from sklearn.metrics import roc_curve
from sklearn.metrics import RocCurveDisplay
y_score = clf.decision_function(X_test)

fpr, tpr, _ = roc_curve(y_test, y_score, pos_label=clf.classes_[1])
roc_display = RocCurveDisplay(fpr=fpr, tpr=tpr).plot()

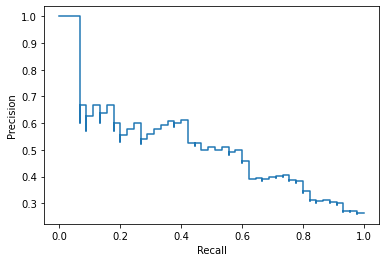
  • 绘制P-R曲线
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import PrecisionRecallDisplay

prec, recall, _ = precision_recall_curve(y_test, y_score,
                                         pos_label=clf.classes_[1])
pr_display = PrecisionRecallDisplay(precision=prec, recall=recall).plot()

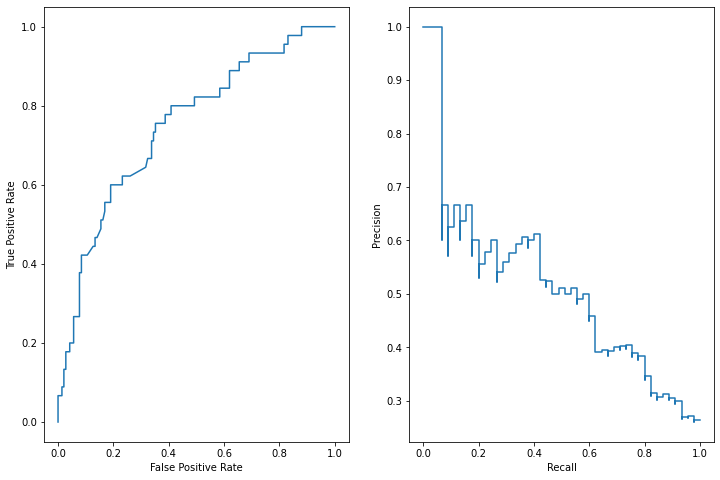
  • 联合展示
import matplotlib.pyplot as plt
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 8))

roc_display.plot(ax=ax1)
pr_display.plot(ax=ax2)
plt.show()

结语

  • sklearn中提供了非常多的算法实现和示例代码，用户只要查阅相关API即可，可节约时间
  • 其实还有很多的模型评估方法，例如西瓜书中还提到了代价敏感错误率与代价曲线，有兴趣的读者可进一步了解

参考资料